Problemática: Google ha decidido dejar de proporcionar una métrica, llamada average position, que determina en qué posición aparecen tus anuncios cuando se realizan búsquedas en Google. Por ello, a partir del 1 de Octubre de 2019, ya no es posible hacer estrategias de pujas ni optimizar campañas basándonos en una posición que ya no tenemos.
Sin embargo, desde Tidart hemos estado buscando la forma de seguir trabajando con esta métrica, incluso sin disponer de ella. Debemos pensar en una forma para calcularla a partir de lo que sí nos ofrece Google: impresiones en la parte superior (% de veces que tu anuncio aparece en el top) e impresiones en la parte superior absoluta (% de veces que tu anuncio aparece de primero).
En Tidart asumimos este reto y comenzamos a desarrollar una solución basada en dos pilares: información previa y algoritmos de machine learning.
Solución: Ante esta situación, debemos utilizar las 2 variables mencionadas que sí nos proporciona Google para intentar estimar la posición media que han eliminado.
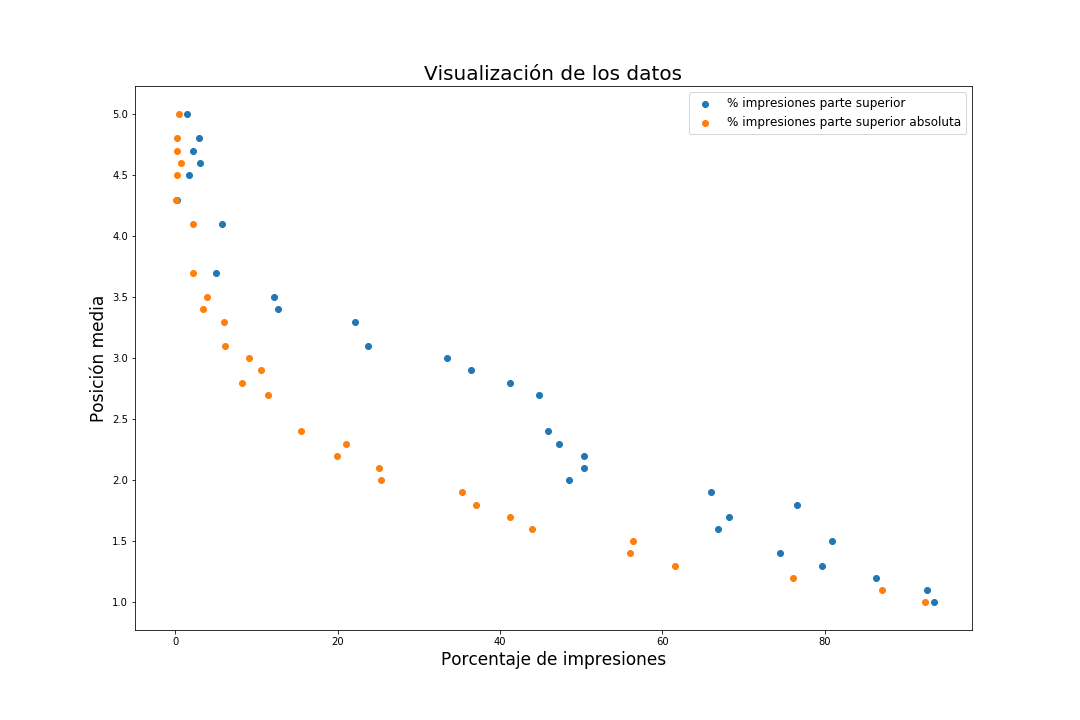
Como primer paso, se han recopilado todos los datos disponibles de campañas de todos los clientes de Tidart clasificados por tipología, tanto de la posición media como de las otras 2 variables, con la intención de descubrir un patrón que las relacione basándonos en los datos reales de nuestro histórico. Después de visualizar estos datos, fue necesario eliminar ciertos valores atípicos que no seguían la lógica de la mayoría.

En esta gráfica se puede observar que, efectivamente, existe relación entre la posición media y cada uno de los porcentajes de impresiones que nos proporciona Google.
Una vez que se tienen claros los datos, empieza la búsqueda del método de machine learning que mejor se ajuste a nuestro problema. Realizamos diversas pruebas empleando 5 algoritmos diferentes: KNN (K-Nearest Neighbors), RF (Random Forest), Multiple linear regression, Polynomial regression y XGBoost.
Desarrollamos su correspondiente hyperparameter tuning para cada uno de los modelos y comparamos tres coeficientes habituales en este campo para decidir cuál era el método que mejor se ajustaba a este caso.
Los tres coeficientes fundamentales empleados para comparar los resultados de las pruebas han sido el error cuadrático medio, el error absoluto medio y el coeficiente de determinación:
| Error cuadrático medio = |  |
, donde N es el tamaño de la muestra. |
| Error absoluto medio = |  |
, donde N es el tamaño de la muestra. |
Coeficiente de determinación, R², que estima la bondad del ajuste.
Finalmente, implementamos la solución en las campañas activas e hicimos un seguimiento del rendimiento del algoritmo. Gracias a haber realizado estos cambios con antelación fuimos capaces de recoger la posición media real y la estimada para valorar la calidad de las estimaciones del algoritmo antes de que Google retirara esta métrica.
Aquí tenemos representadas las posiciones medias reales en azul y las posiciones medias estimadas con el modelo en color naranja. Las zonas sombreadas son los intervalos de confianza asociados a ambas variables.
En la gráfica podemos observar cómo a partir de un nivel, alrededor del 50% de impresiones en la parte superior, la variabilidad se reduce en gran medida y obtenemos estimaciones mucho más precisas.
